小乐数学科普:第9个戴德金数被发现:科学家解决数学中长期存在的问题

德国帕德博恩大学和荷语区鲁汶大学(KU Leuven)的科学家用一个42位的数字创造了历史,用所谓的第九个戴德金数解开了几十年的数学之谜。
作者:帕德博恩大学(Paderborn大学) 2023-6-26
译者:zzllrr小乐(数学科普微信公众号)2023-6-28
自1991年以来,世界各地的专家一直在寻找这个数值。帕德博恩的科学家们在位于那里的Noctua超级计算机的帮助下得出了确切的数列。研究结果将于9月在挪威举行的布尔函数及其应用国际研讨会(BFA,Boolean Functions and their Applications)上公布。

始于Lennart Van Hirtum(上图)的硕士论文项目(当时他是荷语区鲁汶大学的计算机科学学生,现在是帕德博恩大学的研究助理),已经取得了巨大的成功。科学家们加入了一个杰出的团体。该数列的早期数字是由数学家理查德·戴德金(Richard Dedekind)在1897年定义问题时自己发现的,后来由兰道夫·丘奇(Randolph Church)和摩根·沃德(Morgan Ward)等早期计算机科学大师发现。“32年来,D(9)的计算是一个公开的挑战,是否有可能计算出这个数字是值得怀疑的,”Van Hirtum说。
戴德金数列中的前一个数字,即第8个戴德金数,是在1991年使用当时最强大的超级计算机Cray 2发现的。“因此,我们似乎可以想象,现在应该可以在大型超级计算机上计算第 9 个数字,”Van Hirtum 说,描述了这个雄心勃勃的项目的动机,他最初与他在荷语区鲁汶大学的硕士论文导师共同实施。
沙粒、国际象棋和超级计算机
戴德金数的主要主题是所谓的单调布尔函数(monotone Boolean functions)。Van Hirtum解释说:“基本上,你可以将二维、三维和无限维的单调布尔函数视为具有n维立方体的游戏。在一个角上平衡立方体,然后将剩余的每个角着色为白色或红色。只有一条规则:切勿在红色角上方放置白角。这创造了一种垂直的红白相交。
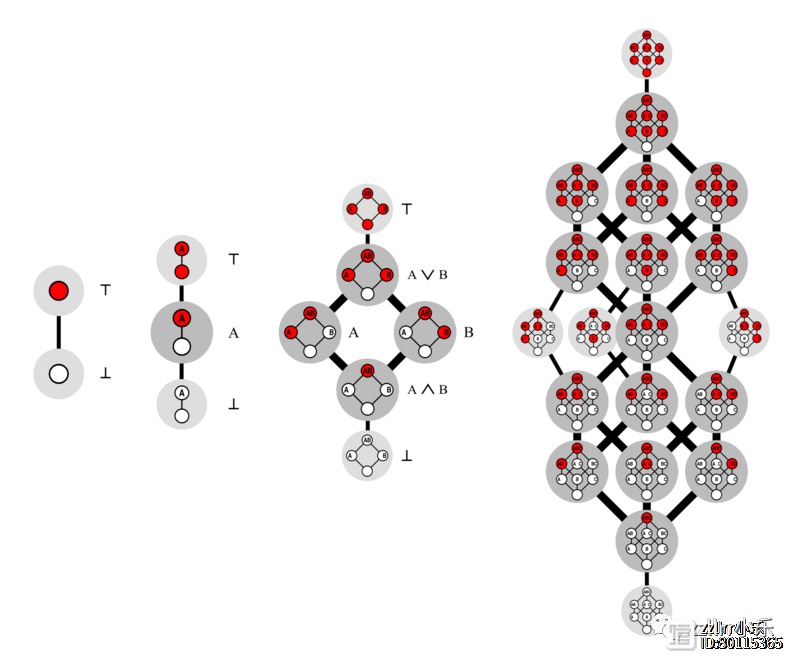
该图显示了0、1、2和3维的所有可能截面。可以制作的这些彩色2维、3维、n维截面的数量被定义为戴德金数(Dedekind数)。
“游戏的目的是计算有多少不同的切割。它们的数量就是戴德金数。即使看起来不像,但这些数字在这个过程中会很快变得巨大:第 8 个戴德金数字已经有 23 位数字(56130437228687557907788)。
相对较大的数字 - 但无比容易计算 - 数字是从关于国际象棋游戏发明的传说中知道的。“根据这个传说,国际象棋游戏的发明者只要求国王在棋盘的每个方格上提供几粒米作为奖励:第一个方格一粒,第二个方格两粒,第三个方格四粒,接下来的每个方格上两倍。国王很快意识到这个要求是不可能实现的,因为全世界都不存在这么多大米。
“整个棋盘上的米粒数将有20位数字 - 这是一个难以想象的数量,但仍然少于D(8)。当你意识到这些数量级时,很明显需要一种有效的计算方法和一台非常快的计算机来找到D(9),”Van Hirtum说。
里程碑:年变成月
为了计算D(9),科学家们使用了硕士论文导师Patrick De Causmaecker开发的一种技术,称为P系数公式(P-coefficient formula)。它提供了一种计算戴德金数的方法,不是通过计数,而是通过非常大的求和。这使得 D(8) 在普通笔记本电脑上只需八分钟即可解码。但是,“D(8)需要八分钟的东西变成了D(9)的数十万年。即使你专门使用大型超级计算机来完成这项任务,完成计算仍然需要很多年,”Van Hirtum指出。
主要问题是这个公式中的项数增长得非常快。“在我们的案例中,通过利用公式中的对称性,我们能够将项的数量减少到'仅仅’5.5x10¹⁸——数量巨大。相比之下,地球上的沙粒数量约为7.5x10¹⁸,这没什么好轻视的,因为对于现代超级计算机来说,5.5x10¹⁸操作非常易于管理,”这位计算机科学家说。
问题:在普通处理器上计算这些项的速度很慢,而且使用 GPU 作为目前许多 AI 应用程序最快的硬件加速器技术对于该算法来说效率不高。
解决方案:使用高度专业化和并行的算术单元(即所谓的FPGA - Field Programmable Gate Array 现场可编程门阵列)的特定应用硬件。Van Hirtum为硬件加速器开发了初始原型,并开始寻找具有必要FPGA卡的超级计算机。在这个过程中,他注意到了帕德博恩大学“帕德博恩并行计算中心(PC2)”的Noctua 2计算机,该计算机拥有世界上最强大的FPGA系统之一。

PC2负责人Christian Plessl博士教授解释说:“当Lennart Van Hirtum和Patrick De Causmaeker与我们联系时,我们立即意识到我们希望支持这个大胆的创新计划项目。用FPGA解决困难的组合问题是一个很有前途的应用领域,Noctua 2是全球为数不多的实验可行的超级计算机之一。极高的可靠性和稳定性要求也对我们的基础设施提出了挑战和考验。FPGA专家咨询团队与Lennart密切合作,根据我们的环境调整和优化应用。
经过几年的开发,该程序在超级计算机上运行了大约五个月。然后时间到了:8月9日,科学家们发现了第9个戴德金数:286386577668298411128469151667598498812366。
至此,戴德金数D(n)前几个( 0 ≤ n ≤ 9)确切值已知为:
D(0)=2
D(1)=3
D(2)=6
D(3)=20
D(4)=168
D(5)=7581
D(6)=7828354
D(7)=2414682040998
D(8)=56130437228687557907788
D(9)=286386577668298411128469151667598498812366
(OEIS 中的序列 A000372 /A000372)
如今,在戴德金项目开始三年后,Van Hirtum正在帕德博恩并行计算中心担任NHR研究生院的研究员,在他的博士学位中开发下一代硬件工具。NHR(national es hochleistungs rechnen 德国国家高性能计算)研究生院是NHR中心的联合研究生院。他将于6月27日下午2点在帕德博恩大学O2演讲厅与Patrick De Causmaecker一起报告他的非凡成功。
参考资料:
/en/event-item/9-dedekind-zahl-entdeckt-wissenschaftler-der-unis-paderborn-leuven-loesen-langbekanntes-problem-der-mathematik-1
/news/2023-06-ninth-dedekind-scientists-long-known-problem.html
/A000372
/wiki/Dedekind_number
让数学
更加
易学易练,
易教易研,
易赏易玩,
易见易得,
易传易及。
上船前必须学会的船舶工作英语
一,舵令1.Portten(five,fifteen,sixteendegrees).左舵十(五、十五、十六)度。2.Starboardten.右舵十度。3.Hardport.左舵满。4.Hardstarboard.右舵满。5.Midshiporamidships.正舵。诺哈网2023-08-26 09:43:450000用英语原版教材轻松揭穿专业词汇的神话
学习过英语单词water(水)的小朋友,肯定能从下面的截图中的“Watermolecule(水分子)”中认识它。同时,也可以猜出来:molecule表“分子”。【英语】water[ˈwɔːtə]n.水拆解:water。请家长朋友大概了解一下词源:From诺哈网2023-08-03 12:16:330000世界五大学习方法之费曼技巧:跟着清华学霸一起高效学习
费曼技巧是世界五大学习方法之一,其他四种分别是:西蒙学习法、番茄工作法、思维导图学习法和跨界学习法。番茄工作法我在工作和孩子的学习中是经常使用的,他也觉得,这种方式比较方便。但我发现,他的学习效率,其实还不是很高,有些知识点,看起来掌握了,但却没很扎实,经常考试就“露馅”了。诺哈网2023-07-31 11:27:100000科教版2023年四年级科学下册期末检测卷(附答案)
一、选择题(24分)1.如图,仙人掌的叶子就像一根刺,它适合生长()的环境中。A.炎热少雨B.寒冷干燥C.炎热多雨2.能改良土壤,并能使土壤肥沃的小动物是()。A.蚯蚓B.蜗牛C.蚂蚁3.科学课上,老师对土壤进行加热,一段时间后发现试管口出现“白气”,说明土壤中含有()。A.空气B.水分C.黏土4.将分别装有岩石、沙、黏土的布袋浸入水中,装有(诺哈网2023-08-05 11:27:260000柯西不等式的待定系数法配凑,如探囊取物,巧解高考最值问题
诺哈网2023-08-23 17:20:200000