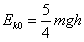圆锥曲线三角形面积与四边形面积题型全归类

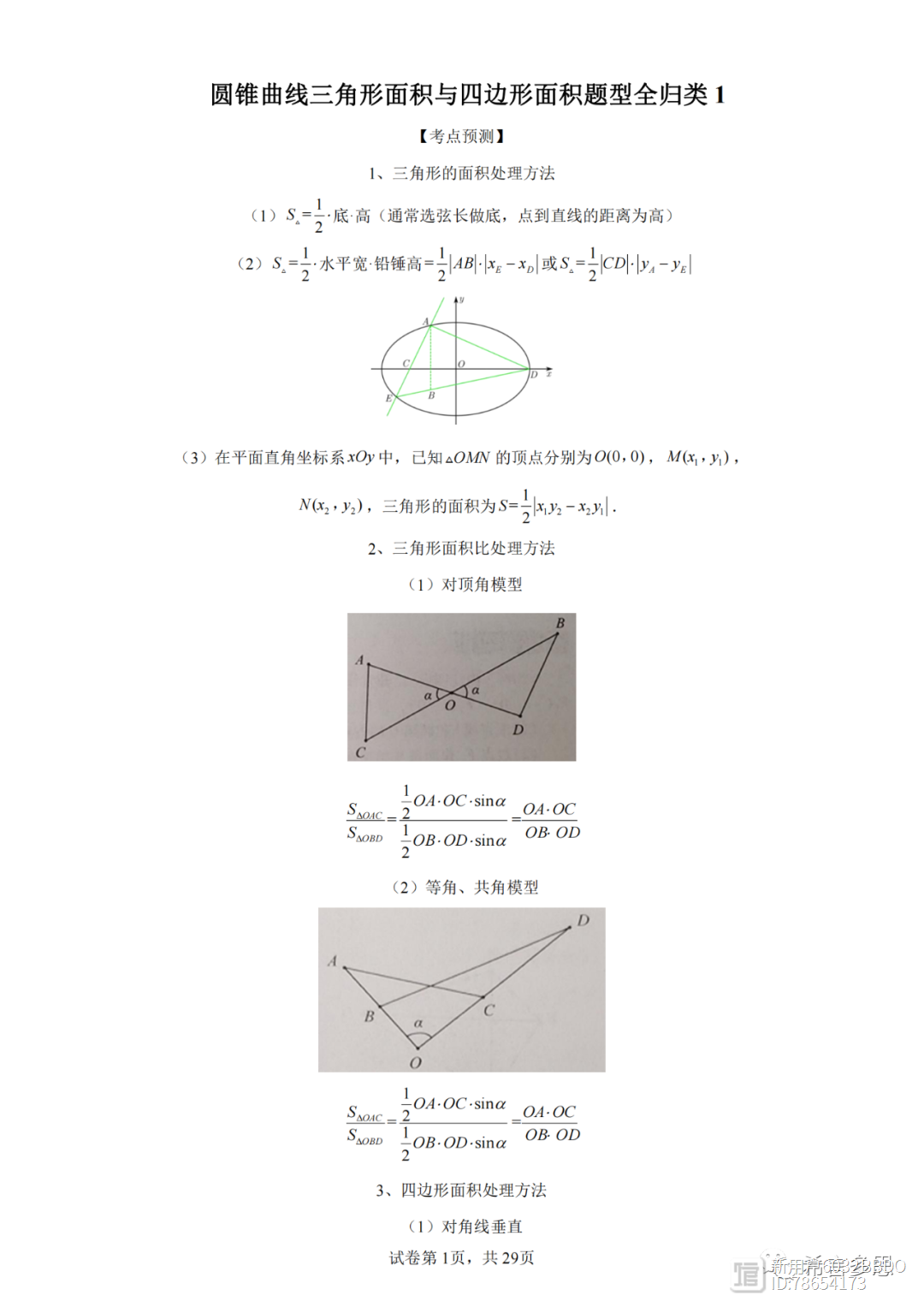
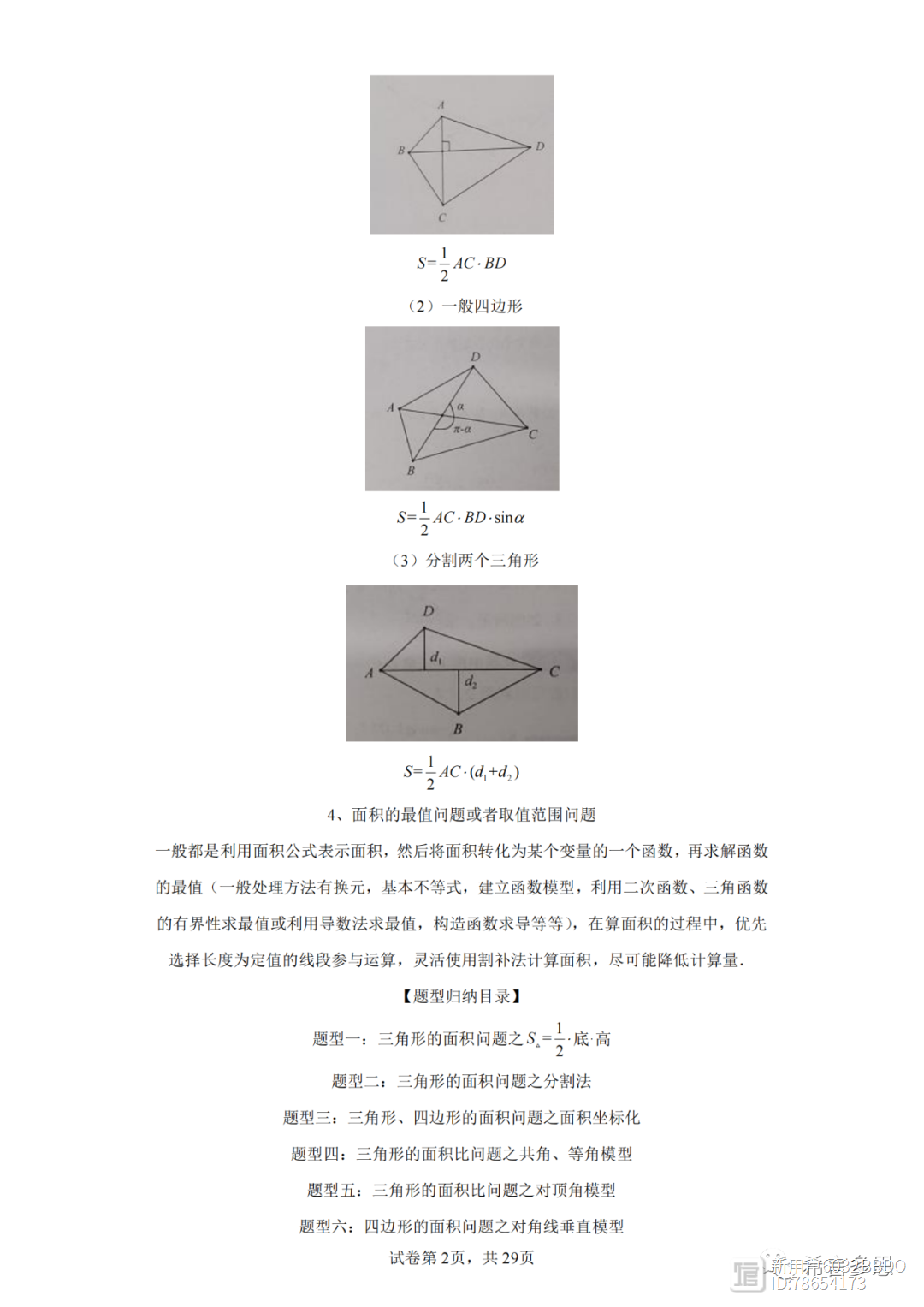
4、面积的最值问题或者取值范围问题

一般都是利用面积公式表示面积，然后将面积转化为某个变量的一个函数，再求解函数的最值（一般处理方法有换元，基本不等式，建立函数模型，利用二次函数、三角函数的有界性求最值或利用导数法求最值，构造函数求导等等），在算面积的过程中，优先选择长度为定值的线段参与运算，灵活使用割补法计算面积，尽可能降低计算量．

【题型归纳目录】

题型一：三角形的面积问题之底·高

题型二：三角形的面积问题之分割法

题型三：三角形、四边形的面积问题之面积坐标化

题型四：三角形的面积比问题之共角、等角模型

题型五：三角形的面积比问题之对顶角模型

题型六：四边形的面积问题之对角线垂直模型

题型七：四边形的面积问题之一般四边形

【典例例题】

题型一：三角形的面积问题之底·高

（2022·上海市复兴高级中学高三开学考试）

1．已知椭圆的离心率为，其左焦点到点的距离为．

(1)求椭圆的方程；

(2)直线与椭圆相交于两点，求的面积关于的函数关系式，并求面积最大时直线的方程．

【答案】(1)

(2)，，直线的方程为.

【分析】（1）利用题干条件列出方程，求出，进而计算出，写出椭圆方程；

（2）联立直线与椭圆方程，得到两根之和，两根之积，利用韦达定理求出弦长，进而求出点到直线距离，表达出面积，并用导函数求解最大值及面积取得最大值时直线的方程.