高中数学三角函数应知应会必记公式汇总
高中数学三角函数应知应会必记公式汇总
1弧度制(必记)
角α的弧度数公式
|α|= (l表示弧长)
角度与弧度的换算
① 1°=rad;②
1 rad=
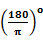
弧长公式
l=|α|r
扇形面积公式
S=
l r=|α|r2
2任意角的三角函数定义(必记)
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么
正弦sinα=y,余弦cosα=x,正切tanα=(x≠0).
设α是一个任意角,它的终边上任意一点P(x,y),记r=
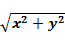
,那么
正弦sinα=
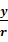
,余弦cosα=

,正切tanα=
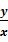
(x≠0).
3同角三角函数的基本关系式(必记)
(1)平方关系:sin2α+cos2α=1.
(2)商数关系:=tanα (α≠+kπ,k∈Z).
4诱导公式(必记)

公式
一
二
三
四
五
六
角
2kπ+α
(k∈Z)
π+α
-α
π-α
-α
+α
正弦sin
sinα
-sinα
-sinα
sinα
cosα
cosα
余弦cos
cosα
-cosα
cosα
-cosα
sinα
-sinα
正切tan
tanα
tanα
-tanα
-tanα
口诀
函数名不变,符号看象限
函数名改变
符号看象限
奇变偶不变,符号看象限
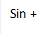

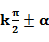
,(k∈Z)

符号规律:


第一象限全“ ”,第二象限sin“ ”,
第三象限tan“ ”,第四象限cos“ ”
[0,2π]特殊角三角函数值(锐角与坐标轴角的函数值必记)(必记)

5和角、差角公式(必记)


6二倍角公式(必记)

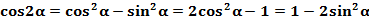

二倍角公式有以下常用变形结论:(规律:升幂缩角,降幂扩角)(会推导)
1、升幂公式:
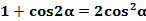

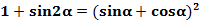

2、降幂公式:

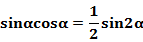
3、正余弦的和差与积结构互化
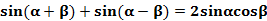
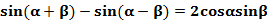

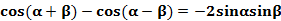
4、正切的和差与积结构互化


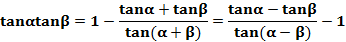
5、倍半关系弦切互化

7半角公式(熟悉其中一组即可)(会推导)
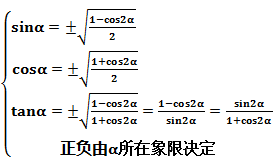
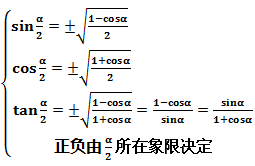
8万能公式(可以理解为二倍角公式的另一种形式)(会推导)
万能公式告诉我们,单角的三角函数都可以用半角的正切来表示。
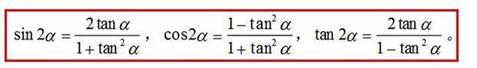
万能公式推导思路:

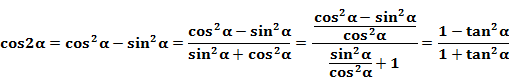

9和差化积公式(会推导)
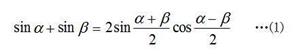
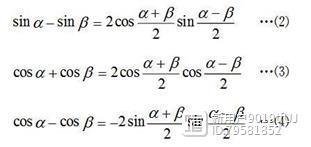
了解和差化积公式的推导,有助于我们理解并掌握好公式:

10积化和差公式(会推导)
我们可以把积化和差公式看成是和差化积公式的逆应用。
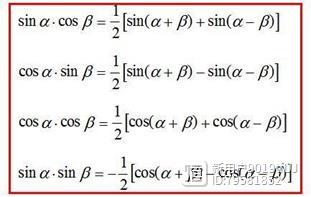
11辅助角公式(必记)

12正弦定理(必记)
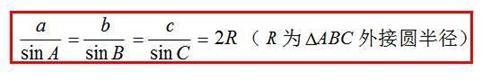
13余弦定理(必记)

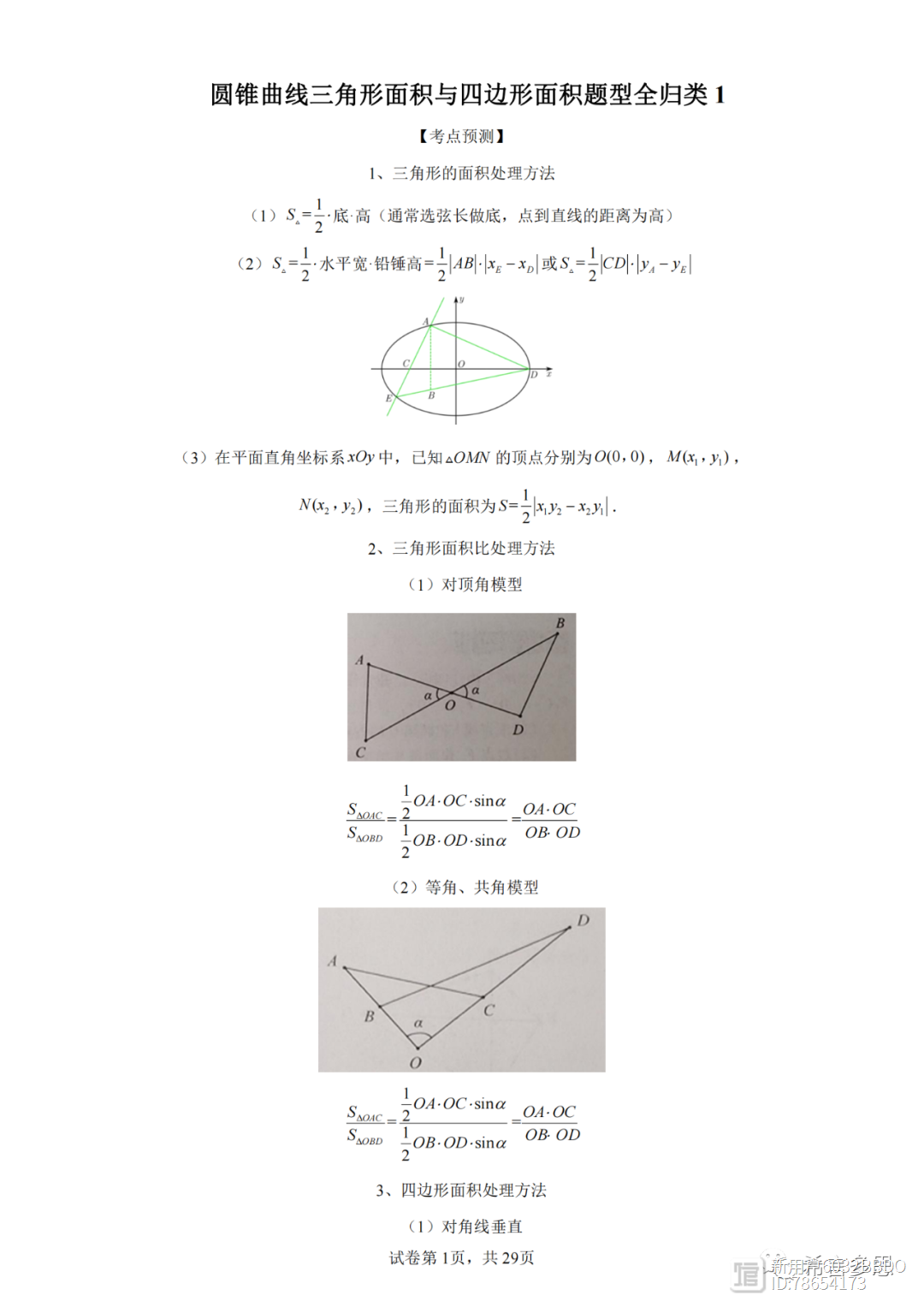
14三角形的面积公式(必记)

说明:
三角问题解题思路的三个转化方向:
1、转化角:分析角的和差倍半关系、异角化同角、非特殊角化特殊角。
2、转化函数名:异名化同名、弦切互化、正余弦互化。
3、转化结构:凑公式结构、和差与积结构的互化、升幂或降幂、因式分解、配完全平方、分式的合并与拆分,整式与分式的互化,出根号,分母有理化、通分、消项、去分母等代数式恒等变形方法与三角公式的分解合并的灵活结合。
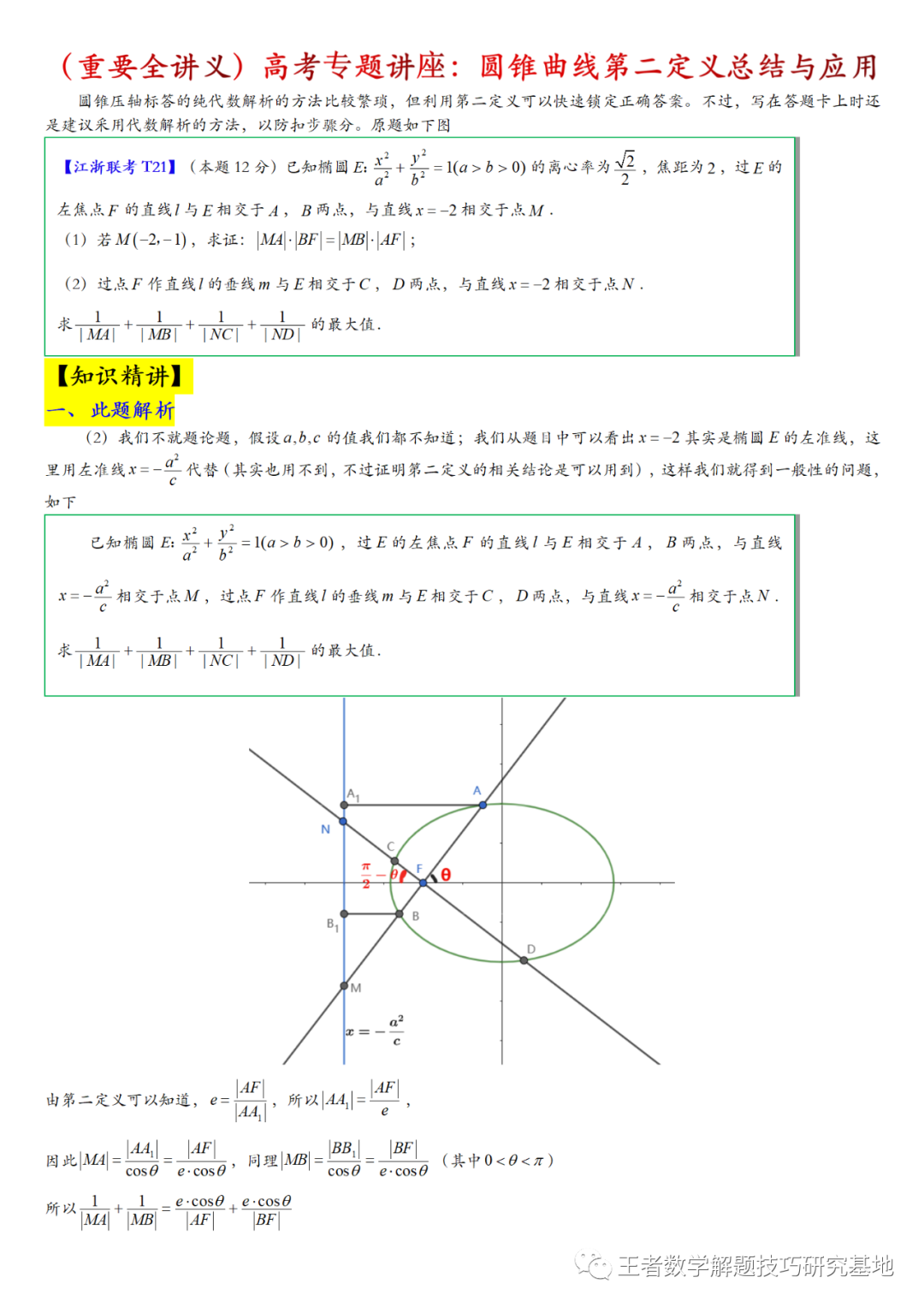
趣味几何 | 三角形中的角格点问题
定义:如果三角形的三个角的度数都是10°的整数倍,三角形内一点与三角形的三个顶点分别联结后,得到的所有的角也都具有这个性质,我们称这样的点为三角形中的角格点.一题多解|再看构造等边三角形的妙用一题多解|5种辅助线求解等腰三角形角度之前写过两篇解题的方法,其实本质上就是三角形的角格点问题,今天我们深入的来研究一下角格点问题。诺哈网2023-08-19 15:33:110000高中【数学】<圆与方程>选择填空题型总结
诺哈网2023-08-03 08:56:580000