来解题吧 | 平行四边形的构造

典型例题1

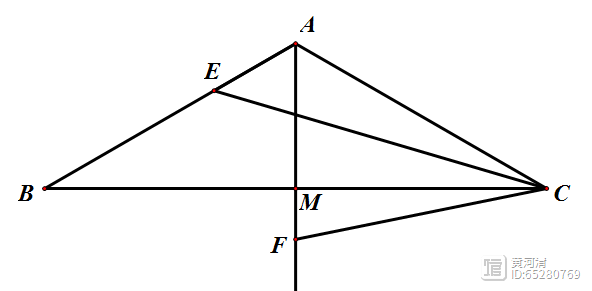
在Rt△ABC中，∠C=90°，D、E分别为CB、CA延长线上的点，BE与AD的交点为P．若BD=AC，AE=CD求∠APE的度数．

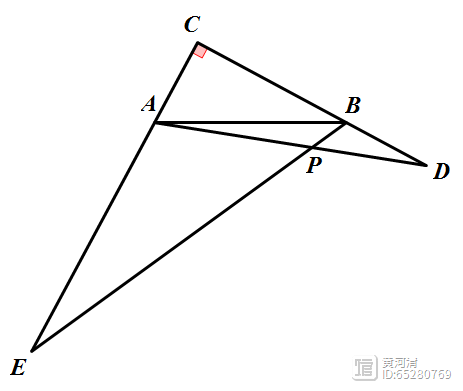
辅助线：过点A作AF⊥AC，且AF=AC。

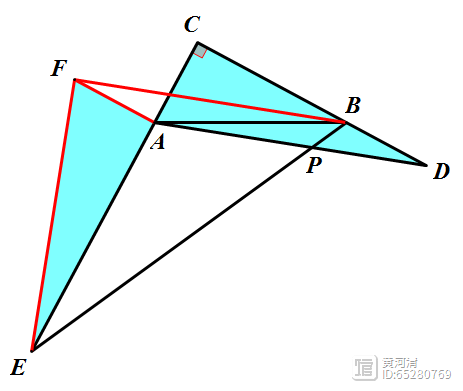
则可以证到△FAE≌△ACD（SAS），从而得到∠1=∠2，EF=BF。

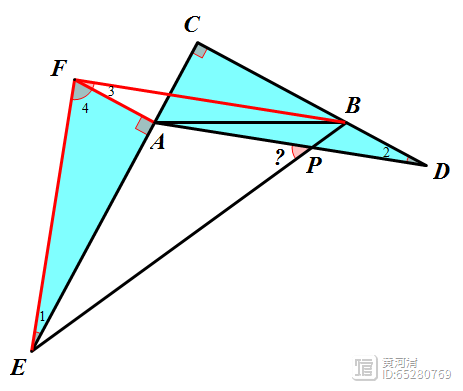
因为AF⊥CE，CD⊥CE，所以AF∥CD

又因为AF=AC，AC=BD，所以AF平行且等于BD，所以四边形AFBD为平行四边形。

所以∠2=∠3，FB=AD。所以∠1=∠2=∠3，FB=AD=EF。因为∠1 ∠4=90°，所以∠3 ∠4=90°，所以△FEB为等腰直角三角形。所以∠FEB=∠FBE=45°因为AD∥FB，所以∠APE=∠FBE=45°。

同理，还有以下辅助线作法，证明思路一致。

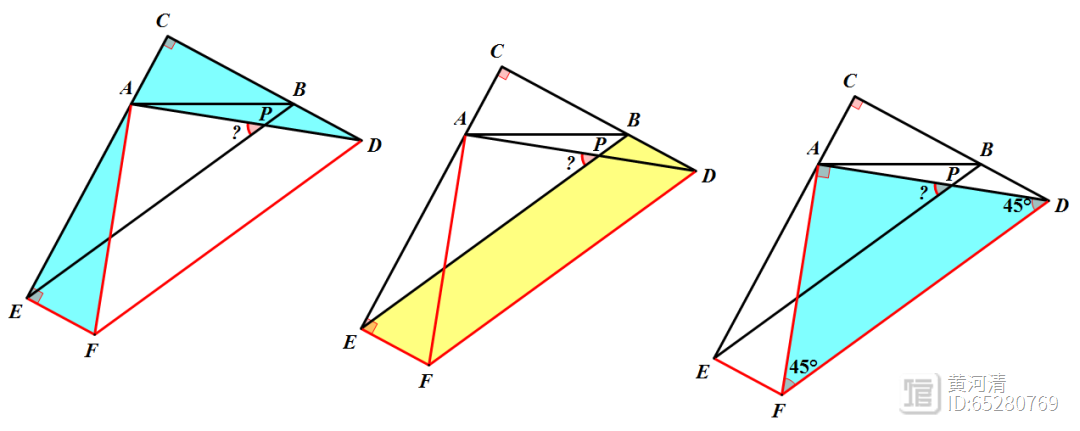
典型例题2

如图，在等腰△ABC中，延长AB到D，延长CA到E，连接DE，恰有AD=BC=CE=DE，求证：∠BAC=100°．

证明思路：

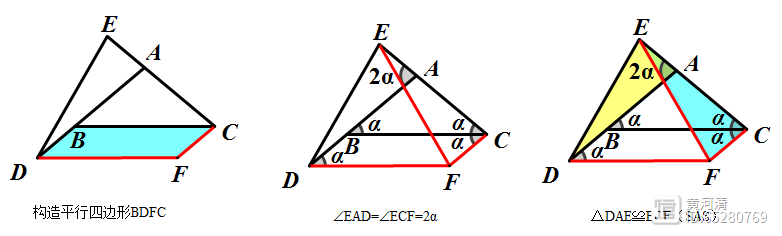
在△ECF中，∠EFC=∠ECF=2α，∠CEF=∠EDA=60°-α

三角形ECF中，内角和为180度

求得α=40°，所以∠BAC=100°

典型例题3

在△ABC中，点P为BC的中点．

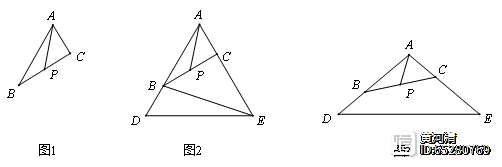
【例1】（1）如图1，求证：AP＜1/2（AB BC）；

（2）延长AB到D，使得BD=AC，延长AC到E，使得CE=AB，连结DE．

①如图2，连结BE，若∠BAC=60°，请你探究线段BE与线段AP之间的数量关系．写出你的结论，并加以证明；

②请在图3中证明：BC≥1/2DE．

此题欢迎思考留言讨论。