2023宁波中考数学压轴题详解，整体难度适中，对多数学生比较友好

(2023宁波中考)如图，以钝角三角形ABC的最长边BC为边向外作矩形BCDE，连接AE、AD，设△AED、△ABE、△ACD的面积为S、S1、S2，若要求出S-S1-S2的值，只需知道( )

A. △ABE的面积 B.△ACD的面积 C.△ABC的面积 D.矩形BCDE的面积

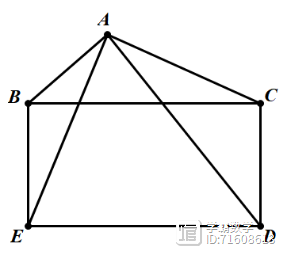
答案：C

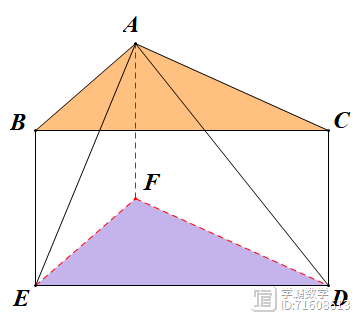
方法一：过点A、E作BE、AB的平行线交于点F，连接DF，易知ABEF、ACDF为平行四边形，EF=AB，DF=AC，DE=BC故△ABC≌△FED，同时△AEF与△ABE面积相等，ADF与ADC面积相等，故S-S1-S2=S△DEF=S△ABC，故选C.

方法二：如图，过点A作AGDE、IJ||DE，设矩形边长分别为a、b，AG=h，AI=c，AJ=a-c,S-S1-S2=

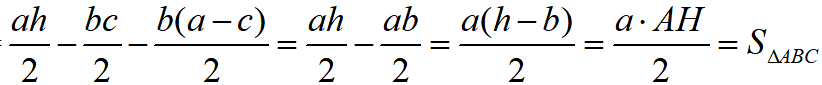
,故选C.

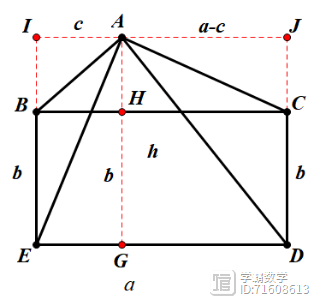
点评：方法一直接通过平行转化，不用计算；而方法二则直接计算，干脆明了.

如图，在Rt△ABC中，∠C=90°，E为AB边上一点，以AE为直径的半圆O与BC相切于点D，连接AD，BE=3

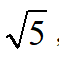
，BD=3，P为AB边上的动点，当△ADP为等腰三角形时，AP的长为________

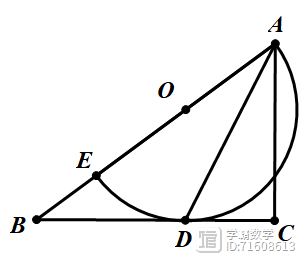
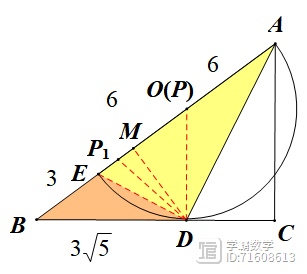
答案：6或2

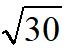
连接OD、DE，易知∠BDE ∠ODE=90°，同时∠ODE ∠ODA=90°得∠BDE=∠ODA，而∠ODA=∠BAD，故∠BDE=∠ABD，于是△BDE~△BAD得BD2=BE·BA得AB=15，于是AE=12同时DE：AD=1：

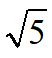
得DE=2

，AD=2

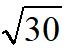
；当PA=PD时，此时P与O重合，故AP=6；当AP=AD时，AP=2

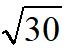
；当DA=DP时，作DMAB于点M，此时易知AM>BM，此时P在AB延长线上，故不符合题意.故AP的长为6或2

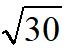
点评：考查圆的切线，相似三角形比较关键，若了解弦切角的概念，那就快很多.

如图，点A、B分别在函数

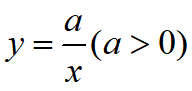
图像的两支上(A在第一象限)，连接AB交x轴于点C，点D、E在函数

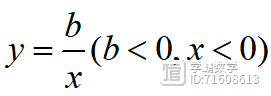
图像上，AE||x轴，BD||y轴，连接DE、BE，若AC=2BC，ABE的面积为9，四边形ABDE的面积为14，则a-b的值为_____，a的值为________

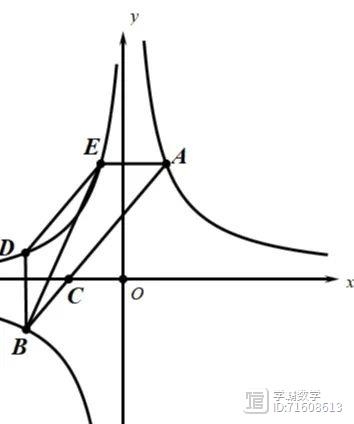
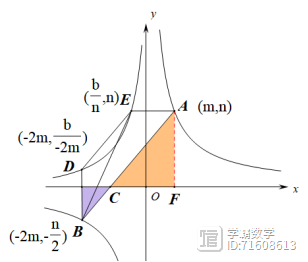
答案：12，9

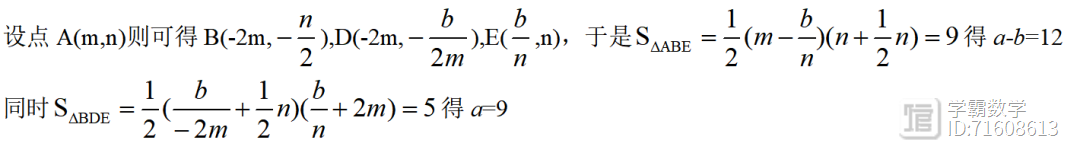
点评：方法还是那个老方法，设点，计算化简整理，考过N多次了，难度并不算大.

如图1，锐角△ABC内接于O，D为BC的中点，连接AD并延长交O于点E，连接BE、CE，过点C作AC的垂线交AE于点F，点G在AD上，连接BG、CG，若BC平分∠EBG且∠BCG=∠AFC

(1) 求∠BGC的度数

(2) 求证：AF=BC

若AG=DF，求tan∠GBC的值；

(3)如图2，当点O恰好在BG上且OG=1，求AC的长.

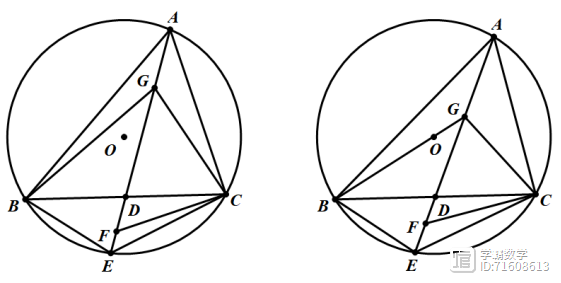
解：(1)∠BGC=90°.设∠CAD=ɑ，则∠CBE=∠BAE=ɑ，而∠ACF=90°得∠AFC=90°-ɑ，∠BCG=∠AFC得∠BCG=90°-ɑ，故∠GBC ∠GCB=90°，故∠BGC=90°

（2）①D为BC的中点，故DG=DC=DB，∠DGC=90°-ɑ=∠CFD，故CF=CG，同时∠CAF=∠CBG，∠ACF=∠BGC，得△ACF≌△BGC，故AF=BC

②设DG=a，则BC=2a，而AF=BC，AG=DF，故DF=AG=

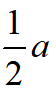
，易知△GCD~△GCF，得CG2=DG·DF得CG=

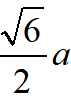
得BG=

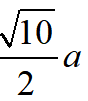
，故tan∠GBC=

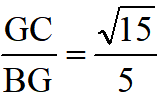
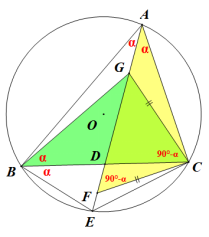
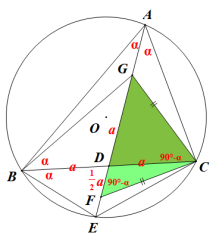
(1) 连接OC，作OI⊥BE于点I，由OB=OC，得OCB=ɑ得OC||BE，故∠COG=∠OBI，得△OGC≌△BIO，故BI=1；同时易得△BDE≌△CDH，CH=BE=2;由OH||BE得GO：GB=OH：BE即有

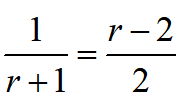
即有

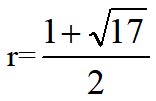
,得AC=BG=

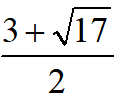
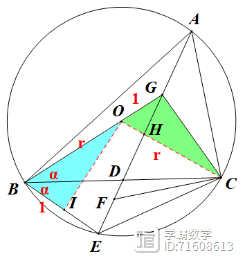
点评：题目最后一问难度较大，图形关系太多，多数同学是处理不过来的；辅助线就有可能挡住多数同学，考查了全等和相似，确实是一道好题.