2023深圳中考数学压轴题详细解析，别以为简单，拿满分很有难度！

(2023深圳中考)10.如图，点P为Rt△ABC(∠B=90°)中，AB与BC上一点，点P从点A出发以2/s的速度运动，A到B后再立即从B到C，到点C时停止，y值为BP的长度，则AC的长为( )

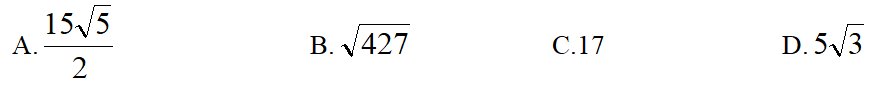
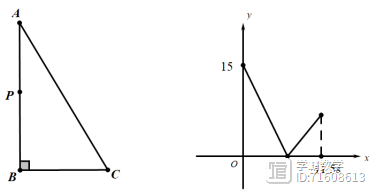
解:由图易知AB=15，而AB BC=11.5×2=23，BC=8，故AC=17，选C.

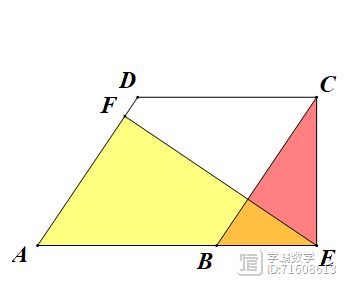
(2023深圳中考)15.如图，已知AB=AC，tan∠B=

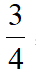
，将△ABD沿AD折叠，且满足AF=3FC(DF>EF),此时

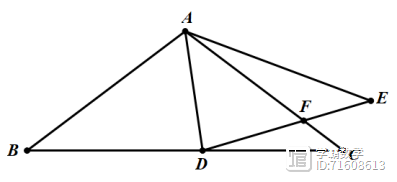
解：方法一：作AG⊥BC、AH⊥DE，易知AG=AH，设AF=3m，则CF=m，AG=

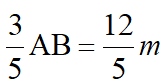
，EH=BG=

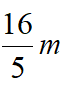
，故FH=

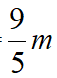
得EF=EH-FH=

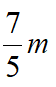
，而由△AEF~△DCF得

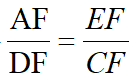
得DF=

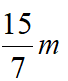
，得

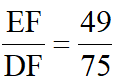
,故

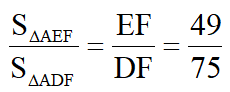
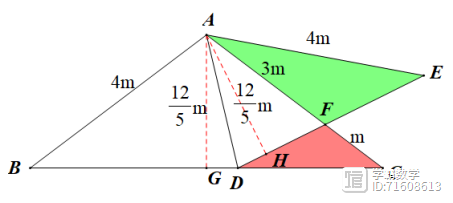
方法二:作FG⊥AE于点G，设CF=1，则AF=3，AC=AE=AB=4，设EF=5m，则FG=3m，GE=4m，在AGF中，有

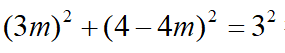
得

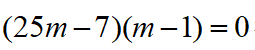
得m=1(舍)或

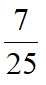
,得EF=

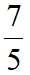
，而由△AEF~△DCF得

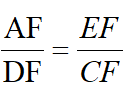
得DF=

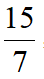
，得

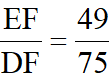
,故

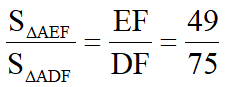
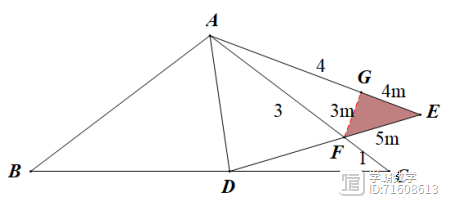
(2023中考数学)22.(1)在矩形ABCD，BE=BC，CF⊥BE，求证：△ABE≌△FCB

当

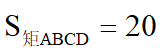
时，求BE·CF=____20_______

(2)菱形ABCD，CE⊥AB，EF⊥AD，cosA=

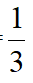
,当

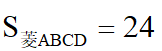
，求EF·BC=_______

(3)平行四边ABCD中，∠A=60°，AB=6，AD=5，CE=2，F为BC上任意一点，作EF⊥EG，交平行四边形ABCD的边于点G，当EF·EG=7

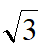
时，直接写出AG的长.

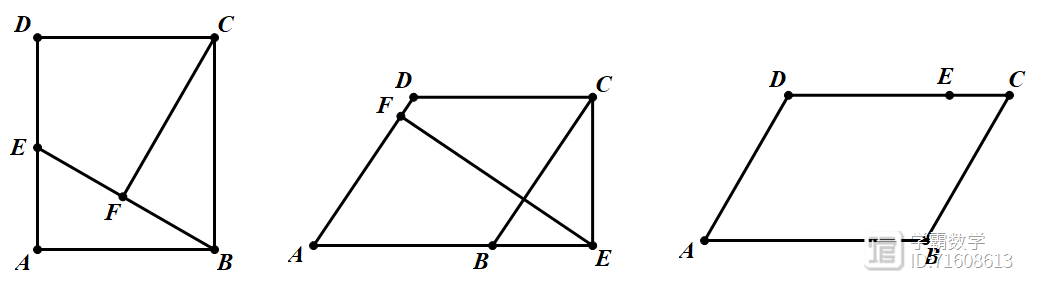
解:(2)易知△AEF~△BCE，得

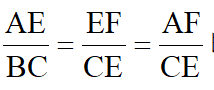
即有AE·CE=EF·BC，而AE=AB BE=AB

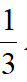
AB=

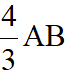
，即EF·BC=

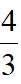
AB·CE=

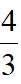
×24=32

(1) ①当点G在AD上时，如图，延长GE交BC延长线于点I，过E作MN⊥AD于点N，交BC于点M，易知△ENG~△FEI，得EF·EG=EN·FI，而EN=2

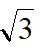
，得FI=

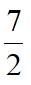
，设FM=m，则MI=

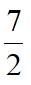
-m，由射影定理得EM2=FM·MI，即有(

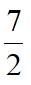
-m)m=3得m=2或

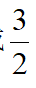
得CI=1或

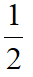
，由DG=2CI得DG=2或1，于是AG=3或4

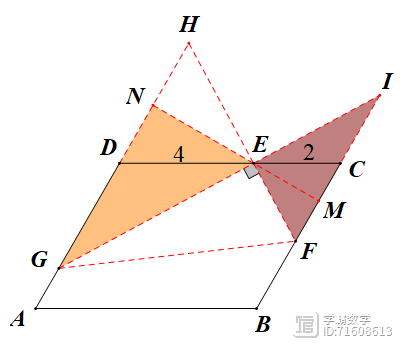
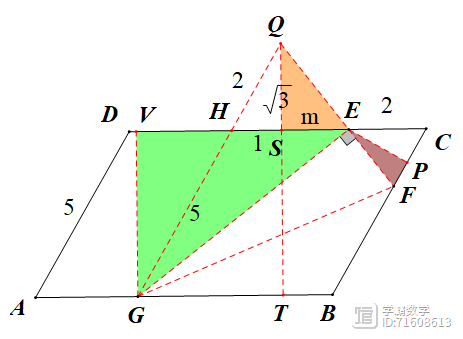
②当G在AB上时，如下左图所示过点G作GQ||AD交FE延长线于点Q，易得△EFP~△GQE得EF·EG=EP·GQ，得GQ=7，得QH=2，作QT⊥AB于点T交CD于点S，作GV⊥CD于点V，设SE=m，由△EQS~△GEV得

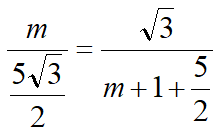
得m=

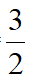
得DH=

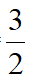
故AG=

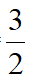
；(亦可由下右图解决，原理一致)

点评：压轴题作图找相似是关键，也是难点所在，第一是画图，可能很多同学不会分类讨论；更难的是相似，相似三角形本身就比较多，同时要直接避开一线三角，重新构造新相似，才能得到EF·EG.

当然，F点能否在BC的延长线上，此时G在BC上，刚开始我还没有意识到还可能会有这种情形，因为题目中的F为BC上任意一点，没有特别明确的说F在线段BC上，但是通过计算发现数据异常复杂.小编认为条件改为F在线段BC上任意一点，会更加严谨.大家觉得呢？欢迎大家分享讨论.

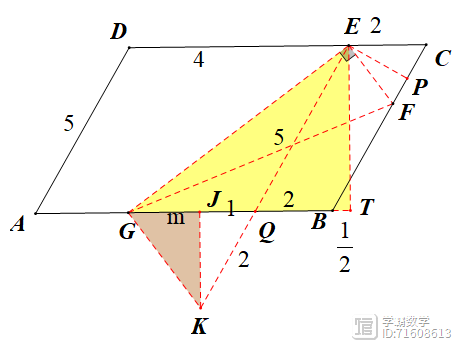
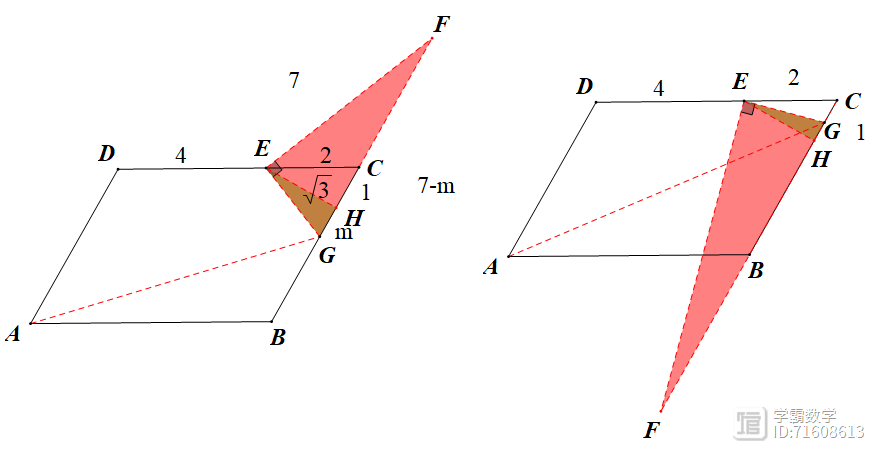
③G在BC上时，此时F在BC的延长线上，如下左右图

左图，易知△EFH~△GFE，得EF·EG=EH·GF，得GF=7，设GH=m得FH=7-m，由射影定理得GH·FH=EH2，即有(7-m)m=3,得m=

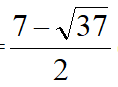
(左图数据)或

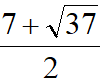
(右图数据)，后续数据过于复杂，交给大家讨论

关于学霸数学

＂学霸数学＂专注于数学中考高考考试的最新信息，好题与压轴题解题技巧、知识专题分析以及考试分析与解答，考试动向及政策分析解读、家庭教育相关分享！如果您是家长或学生，对学习方面有任何问题，请联系小编！