数学数列复习与题目,让你轻松掌握高一上册数学!
数学数列作为高中数学的重要内容之一,不仅在高考中占有一定的比重,而且在日常生活中也有着广泛的应用。本文将为大家带来高一上册数学数列的复习与题目,帮助你轻松掌握这一知识点,为数学学习打下坚实的基础。
一、数列的基本概念回顾
数列是由一系列按照一定规律排列的数所组成的序列。在高一上册数学中,我们主要学习了等差数列和等比数列两种常见的数列类型。在复习数列的基本概念时,我们需要掌握数列的通项公式、前n项和以及求和公式等重要内容。
二、等差数列的复习与题目
1. 等差数列的定义:等差数列是指一个数列中,从第二项开始,每一项与它的前一项之差都相等。
2. 等差数列的通项公式:对于等差数列an,其通项公式为an = a1 (n-1)d,其中a1为首项,d为公差。
3. 等差数列的前n项和公式:对于等差数列an,其前n项和公式为Sn = (a1 an) * n / 2。
4. 等差数列的题目练习:通过解答一些典型的等差数列题目,巩固对等差数列的理解和运用能力。
三、等比数列的复习与题目
1. 等比数列的定义:等比数列是指一个数列中,从第二项开始,每一项与它的前一项之比都相等。
2. 等比数列的通项公式:对于等比数列an,其通项公式为an = a1 * r^(n-1),其中a1为首项,r为公比。
3. 等比数列的前n项和公式:对于等比数列an,其前n项和公式为Sn = a1 * (1 - r^n) / (1 - r)。
4. 等比数列的题目练习:通过解答一些典型的等比数列题目,提高对等比数列的理解和运用能力。
四、数列的应用题
数列在日常生活中有着广泛的应用,比如金融领域的利息计算、人口增长的模型等。通过解答一些数列的应用题,我们可以将数学知识与实际问题相结合,提高解决实际问题的能力。
结语:数学数列作为高中数学的重要内容,掌握好数列的基本概念和运用方法对于学习数学和应对高考都至关重要。通过本文的复习与题目练习,相信大家已经对高一上册数学数列有了更深入的理解。希望大家能够在数学学习中保持积极的态度,勇敢面对挑战,取得优异的成绩!
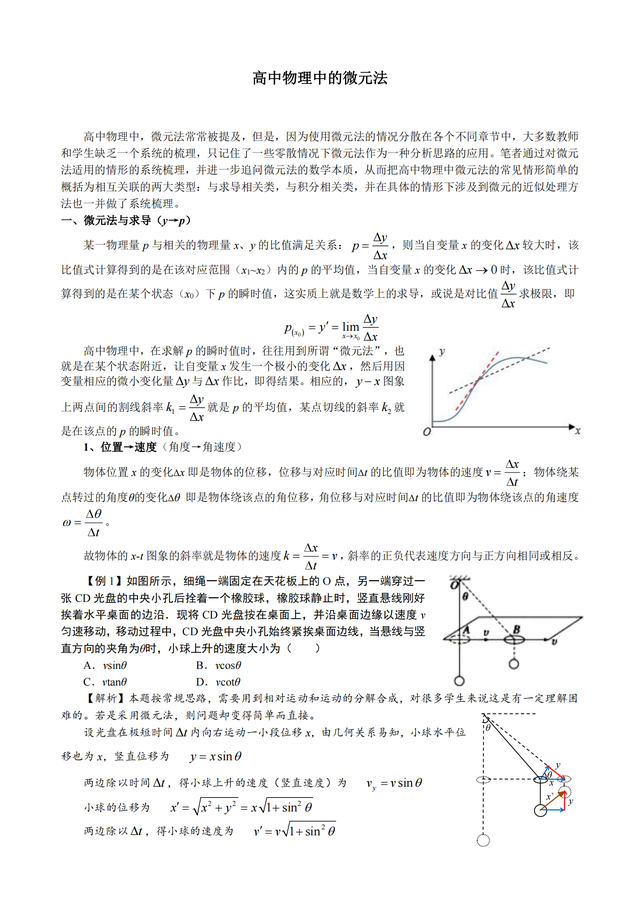
高中物理想拿90分,不会还不知道微元法吧!
高中物理中,微元法常常被提及,但是,因为使用微元法的情况分散在各个不同章节中,大多数教师和学生缺乏一个系统的梳理,只记住了一些零散情况下微元法作为一种分析思路的应用。通过对微元法适用的情形的系统梳理,并进一步追问微元法的数学本质,从而把高中物理中微元法的常见情形简单的概括为相互关联的两大类型:与求导相关类,与积分相关类,并在具体的情形下涉及到微元的近似处理方法也一并做了系统梳理。诺哈网2023-08-25 16:35:230000省钱省时备战中高考:从拉丁语到英语的历史演变
请家长朋友牢记:现代英语60%以上的单词有拉丁语和希腊语根源,在学术上,90%以上的单词源自拉丁语和希腊语。中国孩子学习英语、法语、德语、意大利语、西班牙语的共同任务是认识几百个源自拉丁语和希腊语的常用字。天大的好消息是:我们并不需要刻意学习这些常用字。只要家长朋友大概了解一些词源常识,就可以帮助孩子轻松快速记忆中高考英语词汇。诺哈网2023-08-13 10:36:200000搞笑段子:潘粤明和董洁是不是互相还挂念着对方?智能机器人回答得绝了
人工智能这几天,人工智能聊天机器人ChatGPT横空出世,火遍全网。我搜了一下,说咱国内暂时还用不了,不过我意外发现了很多智能问答机器人。我试着问了一个问题:潘粤明和董洁离婚了,当年互相撕得那么狠毒,可他们以前发布的恩爱动态却一直没删,是不是互相还挂念着对方?机器人回答:不是挂念。我又问:那为什么不删?诺哈网2023-08-05 09:46:160000教育发展现状:小学入学人数增长率跌破0%
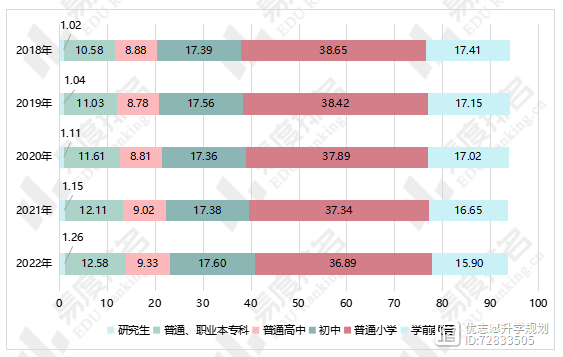
国家统计局于2023年2月28日发布了《中华人民共和国2022年国民经济和社会发展统计公报》,统计公报的教育版块公开了各教育阶段的招生、在学、毕业生的基本情况,本文选取2018-2022年的教育相关数据展示近年我国的教育发展现状。1.2018-2022年各教育阶段在校生人数增加8.8%诺哈网2023-08-07 08:06:590000