交替场中粒子偏转问题

如图所示，在直角坐标系xOy中，第一、四象限内存在三个有界匀强磁场，即垂直纸面向外的匀强磁场Ⅰ、垂直纸面向里的匀强磁场Ⅱ、半径为2L的圆形匀强磁场Ⅲ，匀强磁场Ⅰ、Ⅱ的磁感应强度大小相等，宽均为

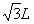
,长均为2L。在第二、三象限存在平行y轴方向的匀强电场Ⅰ、Ⅱ,其电场强度大小相等，方向相反，在第四象限存在匀强电场Ⅲ，其上边界和匀强磁场Ⅲ在M点相切，下边界放置光屏，M点到光屏的垂直距离为

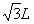
。现有两个质量均为m、带电荷量均为＋q的带电粒子1、2分别从匀强电场Ⅰ、Ⅱ中坐标为

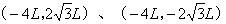
的两点以速度v0沿x轴正方向射出，都恰好经过原点O处分别射人匀强磁场Ⅱ、Ⅰ，又平行于x轴正方向射出匀强磁场Ⅱ、Ⅰ，射人匀强磁场Ⅲ且都从M点射出，最后进入匀强电场Ⅲ打在光屏上。不计粒子的重力及粒子间相互作用，电磁场均具有理想边界。求：（1）匀强磁场Ⅰ、Ⅱ的磁感应强度B1大小；（2）带电粒子1、2在匀强磁场Ⅲ中的运动时间之差Δt；（3）带电粒子1、2最后打在光屏上的距离Δx。

粒子在交替场中的运动问题，适合练手。

场区多、粒子多（两个）、比较的参量多。处理的思路：单个突破，再找联系。

在-x轴区域，两粒子的运动轨迹具有对称性。运动到 x轴区域，在“对称”的磁场区域，两粒子轨迹还具有对称性，进入圆形磁场区域直到运动到M点，实际是一个磁聚焦问题，出磁场区域进入电场区域后，是一个类抛体运动。

从磁场Ⅰ、Ⅱ的右边界射出的粒子，其出射位置到x轴的距离相等，记为y1，两粒子都从磁场的M点射出，且两粒子在磁场中轨迹圆的半径相同。

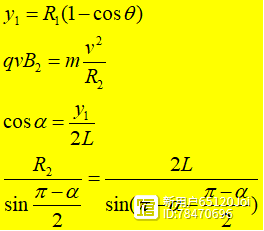
等速同种平行粒子经圆形磁场偏转后从同一点射出磁场，通过分析可知是磁聚焦模型。这种情况下粒子的轨迹圆半径和磁场圆半径相同，利用轨迹圆和磁场圆相交的几何关系。就可以求出两个粒子在磁场中的偏转角，进一步也就知道了粒子进入匀强电场Ⅲ时的速度方向。在匀强电场中做类斜抛运动，将运动沿垂直于光屏方向和平行于光屏方向分解，在光屏上落点的距离也就可知了。

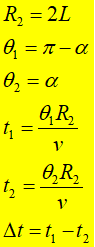
在匀强电场Ⅲ中运动时：

电场力引起的加速度对两粒子运动造成的影响相同，最终两粒子在光屏上的距离不受电场影响。

本题题干文字量大，数据多，场区也多，涉及到的运动类型也多，而且粒子还有两个，运动参量也多，还涉及到两个粒子参量的比较问题。

本题涉及到的运动，实质都比较常规。带电粒子在匀强电场中的类平抛、类抛体运动是常考模型；带电粒子在圆形磁场中的偏转，也比较常见。

成功解决本题，首先需要耐心、细致地审题，场区、已知数据要做好标记，粒子在各区中所做的运动要在图上各区域对应上，最好做好标记。只要熟悉磁聚焦模型，是可以完全破解的。

可能出问题的地方，因为涉及到两个粒子，同一参量有的需要做好标记，下标要分清楚；再就是各个场区的衔接处，坐标、速度一定要分析到位，相对来说比较容易混淆。

通过练习本题，可以帮助学生系统地归纳带电粒子在匀强电场、匀强磁场中常见的运动，进一步熟悉这部分知识。尤其是磁场中的偏转，花样相对比较多，圆形磁场中的问题几何关系相对又复杂一点，通过本题，达到以一题带一类题的效果就好了！